MUVERA: Transforming Multi-Vector Information Retrieval Through Fixed Dimensional Encodings

Posted Jul 8, 2025 Updated Jul 9, 2025

Young man, in mathematics you don’t understand things. You just get used to them. - John von Neumann

By Keyur Ramoliya

39 min read

MUVERA: Transforming Multi-Vector Information Retrieval Through Fixed Dimensional Encodings

Information retrieval systems have become essential components of modern search engines, recommendation systems, and knowledge discovery platforms. These systems help users find relevant documents from massive collections of text data. Traditional retrieval methods relied on simple keyword matching, but recent advances in neural networks have introduced more sophisticated approaches that can understand the meaning and context of both queries and documents.

Neural embedding models have become a fundamental component of modern information retrieval (IR) pipelines [Abstract]. These models transform text into mathematical representations called vectors, which capture semantic meaning in a way that computers can process efficiently. Each document or query becomes a point in a high-dimensional space where similar items are positioned close to each other.

The field of information retrieval has recently witnessed a significant shift from single-vector representations to multi-vector approaches. Single-vector methods produce one embedding per document, allowing for fast retrieval using highly optimized maximum inner product search algorithms. However, recently, beginning with the landmark ColBERT paper, multi-vector models, which produce a set of embedding per data point, have achieved markedly superior performance for IR tasks [Abstract].

Multi-vector models work by creating separate embeddings for each token in a document, rather than compressing the entire document into a single vector. This approach preserves more fine-grained information about the document’s content and structure. ColBERT and its variants produce multiple embeddings per query or document by generating one embedding per token [Section 1]. When comparing a query to a document, these models use a specialized similarity function that considers all possible token-to-token comparisons.

Despite their superior performance, multi-vector models face significant computational challenges. Unfortunately, using these models for IR is computationally expensive due to the increased complexity of multi-vector retrieval and scoring [Abstract]. The computational overhead comes from several factors: the dramatically increased number of embeddings that must be stored and searched, the complexity of the similarity calculations, and the lack of optimized systems designed specifically for multi-vector operations.


From https://arxiv.org/abs/2405.19504

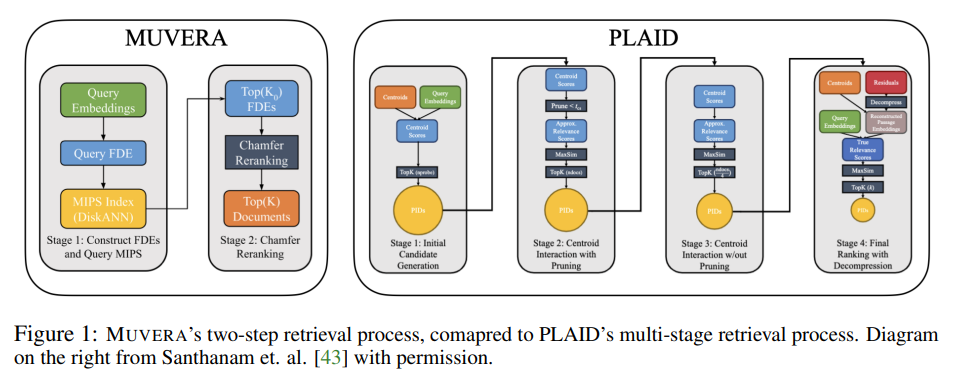
The MUVERA research addresses these computational challenges by introducing a novel approach that bridges the gap between multi-vector performance and single-vector efficiency. In this paper, we introduce MUVERA (Multi-Vector Retrieval Algorithm), a retrieval mechanism which reduces multi-vector similarity search to single-vector similarity search [Abstract]. This transformation enables the use of existing, highly optimized single-vector search systems while maintaining the performance benefits of multi-vector approaches.

Understanding Multi-Vector Retrieval Challenges

The Computational Complexity Problem

Multi-vector retrieval systems face fundamental computational challenges that make them significantly more expensive than their single-vector counterparts. Firstly, producing one embedding per token increases the number of embeddings in a dataset by orders of magnitude [Section 1]. Consider a typical document collection where each document contains dozens or hundreds of tokens. In a single-vector system, each document would be represented by one embedding vector. In a multi-vector system, the same document requires dozens or hundreds of embedding vectors.

The mathematical complexity extends beyond simple storage requirements. Moreover, due to the non-linear Chamfer similarity scoring, there is a lack of optimized systems for multi-vector retrieval [Section 1]. The Chamfer similarity function, which is the standard method for comparing multi-vector representations, requires computing the maximum similarity between each query token and all document tokens. This operation cannot be reduced to simple vector operations that existing search systems handle efficiently.

Specifically, single-vector retrieval is generally accomplished via Maximum Inner Product Search (MIPS) algorithms, which have been highly-optimized over the past few decades [Section 1]. These MIPS algorithms represent decades of optimization work by computer scientists and engineers. They utilize sophisticated data structures, approximation techniques, and hardware-specific optimizations to achieve remarkable speed and efficiency when searching through millions or billions of vectors.

The Single-Vector Heuristic Limitation

Current multi-vector retrieval systems attempt to bridge this efficiency gap through what researchers call the single-vector heuristic. The most prominent approach to MV retrieval is to employ a multi-stage pipeline beginning with single-vector MIPS [Section 1]. This approach tries to leverage existing single-vector search systems by using them as a first-stage filter.

The process works as follows: the basic version of this approach is as follows: in the initial stage, the most similar document tokens are found for each of the query tokens using SV MIPS. Then the corresponding documents containing these tokens are gathered together and rescored with the original Chamfer similarity [Section 1]. This means that for each token in a query, the system searches through all document tokens to find the most similar ones, collects the documents that contain these tokens, and then applies the full multi-vector similarity calculation to this reduced set.

ColBERTv2 and its optimized retrieval engine PLAID are based on this approach, with the addition of several intermediate stages of pruning [Section 1]. PLAID represents the current state-of-the-art in multi-vector retrieval systems and serves as the primary baseline for comparison in the MUVERA research.

However, this heuristic approach has significant limitations. Unfortunately, as described above, employing SV MIPS on individual query embeddings can fail to find the true MV nearest neighbors [Section 1]. The fundamental issue is that finding the most similar individual tokens does not guarantee finding the most similar documents overall. A document might contain tokens that individually match well with query tokens, but the overall document might not be semantically relevant to the query intent.

Additionally, this process is expensive, since it requires querying a significantly larger MIPS index for every query embedding [Section 1]. The index must contain all individual token embeddings from all documents, making it much larger than a single-vector index. Each query requires multiple searches through this expanded index, multiplying the computational cost.

Finally, these multi-stage pipelines are complex and highly sensitive to parameter setting, as recently demonstrated in a reproducibility study, making them difficult to tune [Section 1]. The multiple stages of filtering and rescoring each require careful parameter tuning, and the optimal parameters often depend on the specific dataset and query types being used.

Chamfer Similarity and Multi-Vector Mathematics

Understanding Chamfer Similarity

The mathematical foundation of multi-vector retrieval systems rests on the Chamfer similarity function. Given two sets of vectors Q, P ⊂ $\mathbb{R}^d$, the Chamfer Similarity is given by

\[\operatorname{CHAMFER}(Q, P) = \sum_{q \in Q} \max_{p \in P} \langle q, p \rangle\]

[Section 1.1]. This function captures the intuitive notion that the similarity between two sets of vectors should be determined by how well each vector in the first set can be matched with vectors in the second set.

The Chamfer similarity operates by taking each vector in the query set Q and finding its best match in the document set P using the inner product. The inner product ⟨q, p⟩ measures the cosine similarity between normalized vectors, which indicates how semantically similar two token embeddings are. The maximum operation ensures that each query token is matched with its most compatible document token.

Chamfer similarity is the default method of MV similarity used in the late-interaction architecture of ColBERT, which includes systems like ColBERTv2, Baleen, Hindsight, DrDecr, and XTR, among many others [Section 1.1]. The widespread adoption of this similarity function across multiple research systems demonstrates its effectiveness in capturing meaningful semantic relationships between multi-vector representations.

The historical context of Chamfer similarity extends beyond information retrieval. We note that Chamfer Similarity (and its distance variant) itself has a long history of study in the computer vision and graphics communities, and had been previously used in the ML literature to compare sets of embeddings [Section 1.1]. This cross-disciplinary adoption indicates that the mathematical properties of Chamfer similarity make it suitable for various applications involving set-to-set comparisons.

The Multi-Vector Retrieval Problem Formulation

The formal problem definition for multi-vector retrieval establishes the mathematical framework that MUVERA addresses. In this paper, we study the problem of Nearest Neighbor Search (NNS) with respect to the Chamfer Similarity [Section 1.1]. The nearest neighbor search problem is fundamental in information retrieval, as it directly corresponds to finding the most relevant documents for a given query.

Specifically, we are given a dataset $D = {P_1, \ldots, P_n}$ where each $P_i \subset \mathbb{R}^d$ is a set of vectors [Section 1.1]. Each document in the collection is represented as a set of vectors, typically with one vector per token in the document. The dimensionality d is typically in the range of 64 to 768 dimensions, depending on the embedding model used.

Given a query subset $Q \subset \mathbb{R}^d$, the goal is to quickly recover the nearest neighbor $P^* \in D$, namely:

\[P^* = \arg\max_{P_i \in D} \operatorname{CHAMFER}(Q, P_i)\]

[Section 1.1]. The challenge lies in the word “quickly” - while computing the Chamfer similarity between a query and all documents would give the correct answer, this brute-force approach becomes computationally prohibitive for large document collections.

For the retrieval system to be scalable, this must be achieved in time significantly faster than brute-force scoring each of the $n$ similarities $\operatorname{CHAMFER}(Q, P_i)$ [Section 1.1]. The scalability requirement is crucial for practical applications, where document collections may contain millions or billions of documents, and users expect sub-second response times.

The MUVERA Approach: Fixed Dimensional Encodings

Core Concept and Mathematical Framework

MUVERA introduces a fundamentally different approach to multi-vector retrieval by transforming the problem into a single-vector search problem. MUVERA is a streamlined procedure that directly reduces the Chamfer Similarity Search to MIPS [Section 1.2]. This reduction is achieved through a mathematical transformation that preserves the essential similarity relationships while enabling the use of existing, highly optimized single-vector search systems.

For a pre-specified target dimension $d_{FDE}$, MUVERA produces randomized mappings $F_q : 2^{\mathbb{R}^d} \rightarrow \mathbb{R}^d$ (for queries) and $F_{\text{doc}} : 2^{\mathbb{R}^d} \rightarrow \mathbb{R}^d$ (for documents) [Section 1.2]. These mappings are functions that take a set of vectors as input and produce a single vector as output. The subscripts q and doc indicate that different transformations are used for queries and documents, allowing for asymmetric optimizations.

The key mathematical property that makes MUVERA work is the approximation guarantee: such that, for all query and document multivector representations $Q, P \subset \mathbb{R}^d$, we have:

\[\langle F_q(Q), F_{\text{doc}}(P) \rangle \approx \operatorname{CHAMFER}(Q, P)\]

[Section 1.2]. The inner product between the transformed vectors approximates the original Chamfer similarity, enabling the use of standard MIPS algorithms while preserving the semantic relationships captured by the multi-vector approach.

We refer to the vectors $F_q(Q), F_{\text{doc}}(P)$ as Fixed Dimensional Encodings (FDEs) [Section 1.2]. The term “fixed dimensional” emphasizes that regardless of how many tokens are in the original query or document, the resulting encoding always has the same dimensionality $d_{FDE}$. This property is crucial for efficient indexing and search operations.

The FDE Generation Process

The construction of Fixed Dimensional Encodings involves a sophisticated mathematical process that carefully preserves similarity relationships while reducing dimensionality. The intuition behind our transformation is as follows. Hypothetically, for two MV representations $Q, P \subset \mathbb{R}^d$, if we knew the optimal mapping $π : Q → P$ in which to match them, then we could create vectors $\vec{q},\vec{p}$ by concatenating all the vectors in Q and their corresponding images in P together [Section 2].

This hypothetical scenario would allow perfect preservation of the Chamfer similarity through simple vector concatenation. so that $\langle \vec{q}, \vec{p} \rangle = \sum_{q \in Q} \langle q, \pi(q) \rangle = \operatorname{CHAMFER}(Q, P)$ [Section 2]. However, this ideal approach faces a fundamental challenge: since we do not know $π$ in advance, and since different query-document pairs have different optimal mappings, this simple concatenation clearly will not work [Section 2].

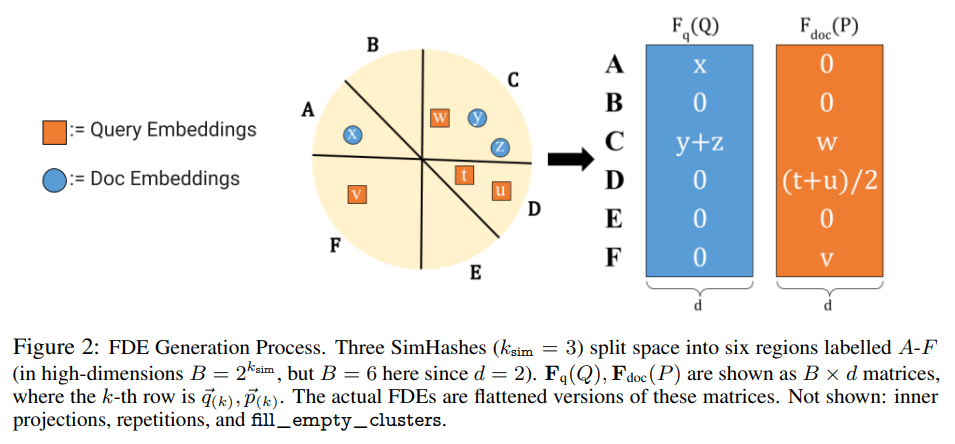
MUVERA overcomes this challenge through a randomized partitioning approach. Instead, our goal is to find a randomized ordering over all the points in $\mathbb{R}^d$ so that, after clustering close points together, the dot product of any query-document pair $Q, P \subset \mathbb{R}^d$ concatenated into a single vector under this ordering will approximate the Chamfer similarity [Section 2].


From https://arxiv.org/abs/2405.19504

The first step in FDE generation involves partitioning the embedding space. The first step is to partition the latent space $\mathbb{R}^d$ into $B$ clusters so that vectors that are closer are more likely to land in the same cluster [Section 2]. This partitioning can be implemented using various clustering methods, with the choice affecting the quality of the final approximation.

Let $\varphi : \mathbb{R}^d \rightarrow [B]$ be such a partition; $\varphi$ can be implemented via Locality Sensitive Hashing (LSH), $k$-means, or other methods [Section 2]. The partition function $\varphi$ assigns each vector to one of $B$ clusters, with the goal that semantically similar vectors are likely to be assigned to the same cluster.

Space Partitioning with SimHash

The choice of partitioning method significantly impacts the quality of the FDE approximation. When choosing the partition function $\varphi$, the desired property is that points are more likely to collide (i.e., $\varphi(x) = \varphi(y)$) the closer they are to each other [Section 2]. This property ensures that the clustering process preserves local similarity relationships.

Such functions with this property exist, and are known as locality-sensitive hash functions (LSH) [Section 2]. LSH functions have been extensively studied in computer science and provide theoretical guarantees about their clustering properties.

For normalized vectors, which are typical in embedding models, when the vectors are normalized, as they are for those produced by ColBERT-style models, SimHash is the standard choice of LSH [Section 2]. SimHash works by using random hyperplanes to partition the vector space, with vectors on the same side of all hyperplanes being assigned to the same cluster.

Specifically, for any $k_{\text{sim}} \geq 1$, we sample random Gaussian vectors $g_1, \dots, g_{k_{\text{sim}}} \in \mathbb{R}^d$, and set $\varphi(x) = (1(\langle g_1, x \rangle > 0), \dots, 1(\langle g_{k_{\text{sim}}}, x \rangle > 0))$ [Section 2]. The indicator function $1(\cdot)$ returns $1$ if the condition is true and $0$ otherwise, creating a binary signature for each vector.

Converting the bit-string to decimal, $\varphi(x)$ gives a mapping from $\mathbb{R}^d$ to $[B]$, where $B = 2^{k_{\text{sim}}}$ [Section 2]. This creates $2^{k_{\text{sim}}}$ distinct clusters, with the number of clusters growing exponentially with the number of random hyperplanes used.

Constructing the Fixed Dimensional Encodings

Once the space partitioning is established, the actual FDE construction involves careful aggregation of vectors within each cluster. After partitioning via $\varphi$, the hope is that for each $q \in Q$, the closest $p \in P$ lands in the same cluster [Section 2]. When this clustering works perfectly, the Chamfer similarity can be decomposed into cluster-wise computations.

If $p$ is the only point in $P$ that collides with $q$, then (1) can be realized as a dot product between two vectors $\vec{q}, \vec{p}$ by creating one block of $d$ coordinates in $\vec{q}, \vec{p}$ for each cluster $k \in [B]$ [Section 2]. This block-wise construction allows the inner product to be decomposed into contributions from each cluster.

However, real-world scenarios often involve multiple vectors mapping to the same cluster. If multiple $p’ \in P$ collide with $q$, then $\langle \vec{q}, \vec{p} \rangle$ will differ from (1), since every $p’$ with $\varphi(p’) = \varphi(q)$ will contribute at least $\langle q, p’ \rangle$ to $\langle \vec{q}, \vec{p} \rangle$ [Section 2]. This situation requires a more sophisticated approach to maintain the approximation quality.

To resolve this, we set $\vec{p}(k)$ to be the centroid of the points $p \in P$ with $\varphi(p) = \varphi(q)$ [Section 2]. Using centroids provides a natural way to aggregate multiple vectors while preserving their collective semantic content. The formal definition involves careful normalization: for $k={1,\dots,B}$,we define[Section 2]

\[\vec{q}(k) = \sum_{\substack{q \in Q \\ \varphi(q) = k}} q, \quad\vec{p}(k) = \frac{1}{|P \cap \varphi^{-1}(k)|} \sum_{\substack{p \in P \\ \varphi(p) = k}} p\]

Setting $\vec{q} = (\vec{q}(1), \dots, \vec{q}(B))$ and $\vec{p} = (\vec{p}(1), \dots, \vec{p}(B))$, then we have

\[\langle \vec{q}, \vec{p} \rangle =\sum_{k=1}^{B} \sum_{\substack{q \in Q \\ \varphi(q) = k}}\frac{1}{|P \cap \varphi^{-1}(k)|}\sum_{\substack{p \in P \\ \varphi(p) = k}}\langle q, p \rangle\]

This mathematical formulation shows how the inner product of the FDEs relates to the original Chamfer similarity.

Dimensionality Reduction and Repetitions

The basic FDE construction results in vectors of dimension $dB$, which may be too large for efficient processing. Note that the resulting dimension of the vectors $\vec{q}, \vec{p}$ is $dB$. To reduce the dependency on $d$, we can apply a random linear projection $\psi : \mathbb{R}^d \rightarrow \mathbb{R}^{d_{\text{proj}}}$ to each block $\vec{q}(k), \vec{p}(k)$, where $d_{\text{proj}} < d$ [Section 2].

Specifically, we define $\psi(x) = \frac{1}{\sqrt{d_{\text{proj}}}} Sx$, where $S \in \mathbb{R}^{d_{\text{proj}} \times d}$ is a random matrix with uniformly distributed entries from ${\pm 1}$ [Section 2]. This random projection technique preserves inner products approximately while reducing dimensionality, based on the Johnson–Lindenstrauss lemma.

To improve the approximation quality, MUVERA uses repetitions with independent randomization. To increase accuracy of (3) in approximating (1), we repeat the above process $R_{\text{reps}} \geq 1$ times independently, using different randomized partitions $\varphi_1, \dots, \varphi_{R_{\text{reps}}}$ and projections $\psi_1, \dots, \psi_{R_{\text{reps}}}$ [Section 2].

We denote the vectors resulting from the $i$-th repetition by $\vec{q}_{i,\psi},\vec{p}_{i,\psi}$. Finally, we concatenate these $R_{\text{reps}}$ vectors together, so that our final FDEs are defined as $F_q(Q) = (\vec{q}_{1,\psi}, \dots, \vec{q}_{R_{\text{reps}},\psi})$ and $F_{\text{doc}}(P) = (\vec{p}_{1,\psi}, \dots, \vec{p}_{R_{\text{reps}},\psi})$ [Section 2].

Observe that a complete FDE mapping is specified by the three parameters $(B, d_{\text{proj}}, R_{\text{reps}})$, resulting in a final dimension of $d_{\text{FDE}} = B \cdot d_{\text{proj}} \cdot R_{\text{reps}}$ [Section 2]. These parameters provide control over the trade-off between approximation quality and computational efficiency.

Handling Empty Clusters

A practical challenge in FDE construction occurs when the partitioning results in empty clusters for certain documents. A key source of error in the FDE’s approximation is when the nearest vector $p \in P$ to a given query embedding $q \in Q$ maps to a different cluster, namely $\varphi(p) \ne \varphi(q) = k$[Section 2].

MUVERA addresses this issue through a technique called “filling empty clusters.” To avoid this trade-off, we directly ensure that if no $p \in P$ maps to a cluster $k$, then instead of setting $\vec{p}(k) = 0$, we set $\vec{p}(k)$ to the point $p$ that is closest to cluster $k$ [Section 2].

Formally, for any cluster $k$ with $P \cap \varphi^{-1}(k) = \emptyset$, if fill_empty_clusters is enabled, we set $\vec{p}(k) = p$, where $p \in P$ is the point for which $\varphi(p)$ has the fewest number of disagreeing bits with $k$ [Section 2]. This approach ensures that every cluster has meaningful content, improving the approximation quality.

We do not enable this for query FDEs, as doing so would result in a given $q \in Q$ contributing to the dot product multiple times[Section 2]. The asymmetric treatment of queries and documents reflects the different roles they play in the retrieval process.

Theoretical Guarantees and Mathematical Analysis

Approximation Quality Guarantees

MUVERA provides rigorous theoretical guarantees for the quality of its approximations. We now state our theoretical guarantees for our FDE construction. For clarity, we state our results in terms of normalized Chamfer similarity $\text{NCHAMFER}(Q, P) = \frac{1}{|Q|}\text{CHAMFER}(Q, P)$ [Section 2.1]. The normalization ensures that the similarity scores fall within a bounded range, simplifying the theoretical analysis.

This ensures $\text{NCHAMFER}(Q, P) \in [-1, 1]$ whenever the vectors in $Q, P$ are normalized. Note that this factor of ${1}/{|Q|}$ does not affect the relative scoring of documents for a fixed query [Section 2.1]. The relative ranking of documents remains unchanged, which is the key property needed for effective retrieval systems.

Our main result is that FDEs give $\varepsilon$-additive approximations of the Chamfer similarity [Section 2.1]. This means that the FDE inner product will be within $\varepsilon$ of the true Chamfer similarity with high probability, providing a formal guarantee about the approximation quality.

Fix any $\varepsilon, \delta > 0$, and sets $Q, P \subset \mathbb{R}^d$ of unit vectors, and let $m = |Q| + |P|$. Then setting $k_{\text{sim}} = O(\frac{\log(m \delta^{-1})}{\varepsilon})$, $d_{\text{proj}} = O(\frac{1}{\varepsilon^2}\log(\frac{m}{\varepsilon \delta}))$, $R_{\text{reps}} = 1$, so that $d_{\text{FDE}} = (m/\delta)^{O(1/\varepsilon)}$, then in expectation and with probability at least $1 - \delta$ we have

\[\text{NCHAMFER}(Q, P) - \varepsilon \leq \frac{1}{|Q|}\langle F_q(Q), F_{\text{doc}}(P)\rangle \leq \text{NCHAMFER}(Q, P) + \varepsilon\]

[Theorem 2.1]. This theorem establishes both upper and lower bounds on the approximation error, showing that the FDE approach provides a faithful representation of the original similarity relationships.

Runtime and Complexity Analysis

The theoretical analysis extends beyond approximation quality to runtime guarantees. Finally, we show that our FDEs give an $\varepsilon$-approximate solution to Chamfer similarity search, using FDE dimension that depends only logarithmically on the size of the dataset $n$ [Section 2.1]. The logarithmic dependence on dataset size is crucial for scalability, as it means the method can handle very large document collections efficiently.

Using the fact that our query FDEs are sparse, one can run exact MIPS over the FDEs in time $\widetilde{O}(|Q| \cdot n)$, improving on the brute-force runtime of $O(|Q| \cdot \max_i |P_i| \cdot n)$ for Chamfer similarity search [Section 2.1]. The sparsity of query FDEs provides additional computational advantages, as sparse vector operations can be performed more efficiently than dense operations.

The formal runtime analysis provides precise bounds on the computational complexity. Fix any $\varepsilon > 0$, query $Q$, and dataset $P = {P_1, \dots, P_n}$, where $Q \subset \mathbb{R}^d$ and each $P_i \subset \mathbb{R}^d$ is a set of unit vectors. Let $m = |Q| + \max_{i \in [n]} |P_i|$. Let $k_{\text{sim}} = O(\frac{\log m}{\varepsilon})$, $d_{\text{proj}} = O(\frac{1}{\varepsilon^2} \log(m / \varepsilon))$ and $R_{\text{reps}} = O(\frac{1}{\varepsilon^2} \log n)$ so that $d_{\text{FDE}} = m^{O(1/\varepsilon)} \cdot \log n$ [Theorem 2.2].

Then if $i^* = \arg\max_{i \in [n]} \langle F_q(Q), F_{\text{doc}}(P_i) \rangle$, with high probability (i.e., $1 - 1/\text{poly}(n)$), we have:

\[\text{NCHAMFER}(Q, P_{i^*}) \geq \max_{i \in [n]} \text{NCHAMFER}(Q, P_i) - \varepsilon\]

[Theorem 2.2]. This guarantee shows that the document found by FDE search is nearly optimal with respect to the true Chamfer similarity.

Given the query $Q$, the document $P^*$ can be recovered in time $O(|Q|\max{d, n}\frac{1}{\varepsilon^4}\log(\frac{m}{\varepsilon})\log n)$ [Theorem 2.2]. This runtime bound provides a concrete estimate of the computational cost, showing that the method scales reasonably with problem parameters.

Experimental Evaluation and Performance Analysis

Dataset and Experimental Setup

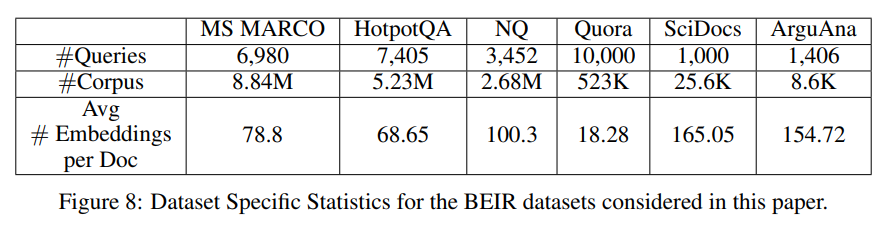
The experimental evaluation of MUVERA uses established benchmark datasets from the information retrieval community. Our evaluation includes results from six of the well-studied BEIR information retrieval datasets: MS MARCO, HotpotQA, NQ, Quora, SciDocs, and ArguAna [Section 3]. These datasets represent diverse domains and query types, providing a comprehensive evaluation of the method’s generalizability.

These datasets were selected for varying corpus size (8K-8.8M) and average number of document tokens (18-165) [Section 3]. The range of dataset sizes and document lengths ensures that the evaluation covers various real-world scenarios, from small specialized collections to large-scale web search scenarios.


From https://arxiv.org/abs/2405.19504

The experimental setup uses state-of-the-art multi-vector models for generating embeddings. We compute our FDEs on the MV embeddings produced by the ColBERTv2 model, which have a dimension of $d = 128$ and a fixed number $|Q| = 32$ of embeddings per query [Section 3]. ColBERTv2 represents the current state-of-the-art in multi-vector retrieval systems, making it an appropriate baseline for comparison.

The number of document embeddings is variable, ranging from an average of 18.3 on Quora to 165 on Scidocs. This results in 2,300-21,000 floats per document on average (e.g. 10,087 for MS MARCO) [Section 3]. The variable document lengths reflect real-world document collections, where document sizes can vary significantly.

FDE Quality Analysis

The experimental evaluation begins with an offline analysis of FDE quality, measuring how well the fixed dimensional encodings approximate the true Chamfer similarity. We evaluate the quality of our FDEs as a proxy for the Chamfer similarity, without any re-ranking and using exact (offline) search [Section 3.1]. This offline evaluation isolates the approximation quality from other system effects.

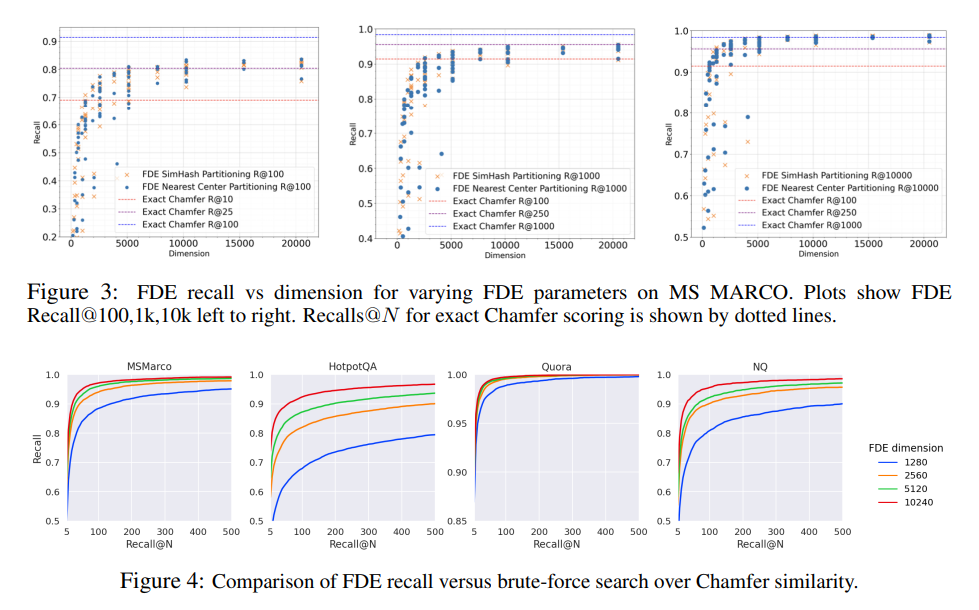
We first demonstrate that FDE recall quality improves dependably as the dimension $d_{\text{FDE}}$ increases, making our method relatively easy to tune [Section 3.1]. The predictable relationship between dimensionality and quality is important for practical deployment, as it allows system designers to choose appropriate parameters based on their performance requirements.


From https://arxiv.org/abs/2405.19504

The parameter sensitivity analysis reveals important insights about FDE construction. We perform a grid search over FDE parameters $R_{\text{reps}} \in {1, 5, 10, 15, 20}$, $k_{\text{sim}} \in {2, 3, 4, 5, 6}$, $d_{\text{proj}} \in {8, 16, 32, 64}$, and compute recall on MS MARCO [Section 3.1]. This comprehensive parameter exploration helps identify the most effective configurations.

We find that Pareto optimal parameters are generally achieved by larger $R_{\text{reps}}$, with $k_{\text{sim}}, d_{\text{proj}}$ playing a lesser role in improving quality [Section 3.1]. This finding suggests that using multiple independent repetitions is more effective than increasing the complexity of individual repetitions.

Specifically, $(R_{\text{reps}}, k_{\text{sim}}, d_{\text{proj}}) \in {(20, 3, 8), (20, 4, 8), (20, 5, 8), (20, 5, 16)}$ were all Pareto optimal for their respective dimensions [Section 3.1]. These parameter combinations provide practical guidance for implementing MUVERA in real systems.

Comparison with Single-Vector Heuristics

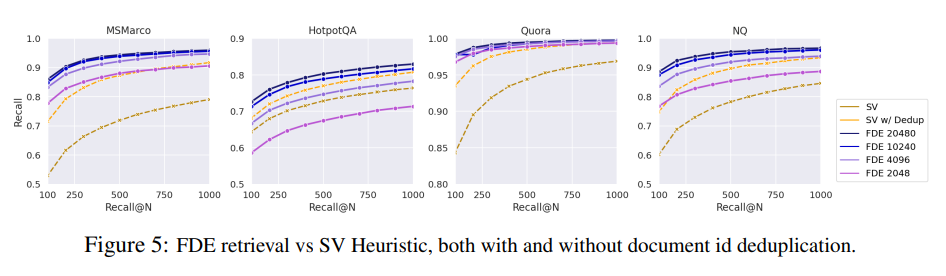
A critical aspect of the evaluation involves comparing MUVERA’s FDE approach with the existing single-vector heuristic used in systems like PLAID. We compare the quality of FDEs as a proxy for retrieval against the previously described SV heuristic, which is the method underpinning PLAID [Section 3.1]. This comparison directly addresses the question of whether FDEs provide a better approximation than existing methods.


From https://arxiv.org/abs/2405.19504

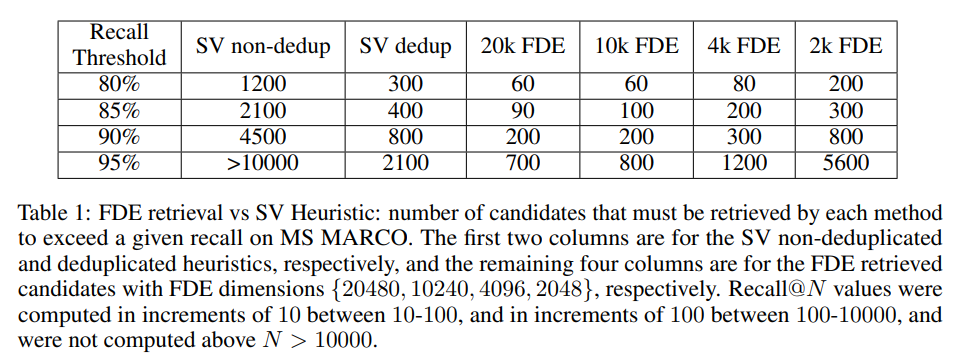
The comparison methodology carefully accounts for the computational costs of different approaches. To compare the cost of the SV heuristic to running MIPS over the FDEs, we consider the total number of floats scanned by both using a brute-force search [Section 3.1]. This metric provides a fair comparison by measuring the fundamental computational work required by each method.

The FDE method must scan $n \cdot d_{\text{FDE}}$ floats to compute the $k$-nearest neighbors. For the SV heuristic, one runs 32 brute-force scans over $n \cdot m_{\text{avg}}$ vectors in 128 dimensions, where $m_{\text{avg}}$ is the average number of embeddings per document [Section 3.1]. The factor of 32 comes from the fixed number of query embeddings in ColBERTv2, and $m_{\text{avg}}$ varies significantly across datasets.

For MS MARCO, where $m_{\text{avg}} = 78.8$, the SV heuristic searches through $32 \cdot 128 \cdot 78.8 \cdot n$ floats. This allows for an FDE dimension of $d_{\text{FDE}} = 322,764$ to have comparable cost! [Section 3.1]. This calculation demonstrates that FDEs can use much higher dimensions than initially expected while remaining computationally competitive.

The empirical results show significant advantages for the FDE approach. On MS MARCO, even the 4096-dimensional FDEs match the recall of the (deduplicated) SV heuristic while retrieving $1.75-3.75 \times$ fewer candidates [Section 3.1]. This improvement in efficiency comes with no loss in retrieval quality, demonstrating the effectiveness of the FDE approach.

For our 10240-dimensional FDEs, these numbers are $2.6-5 \times$ and $20-22.5 \times$ fewer, respectively [Section 3.1]. The higher-dimensional FDEs achieve even greater efficiency improvements, showing that the method scales well with increased computational budget.


From https://arxiv.org/abs/2405.19504

End-to-End System Performance

The evaluation extends beyond offline analysis to measure end-to-end system performance in realistic deployment scenarios. We implemented MUVERA, an FDE generation and end-to-end retrieval engine in C++ [Section 3.2]. The implementation includes various optimizations that are crucial for practical deployment.

Our single-vector retrieval engine uses a scalable implementation of DiskANN, a state-of-the-art graph-based ANNS algorithm [Section 3.2]. DiskANN represents one of the most efficient approximate nearest neighbor search systems available, providing a strong foundation for the MIPS operations required by MUVERA.

We build DiskANN indices by using the uncompressed document FDEs with a maximum degree of 200 and a build beam-width of 600 [Section 3.2]. These parameters represent a balance between index construction time and search quality, based on established best practices for DiskANN deployment.

The system includes several practical optimizations that improve real-world performance. To improve re-ranking speed, we reduce the number of query embeddings by clustering them via a ball carving method and replacing the embeddings in each cluster with their sum [Section 3.2]. This optimization reduces the computational cost of the final re-ranking step without sacrificing accuracy.

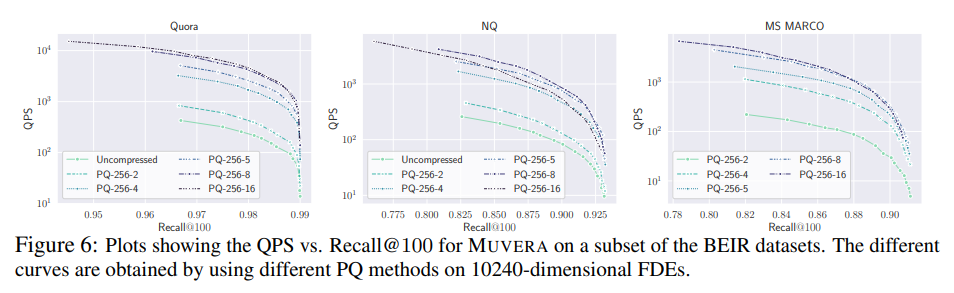
To further improve the memory usage of MUVERA, we use a textbook vector compression technique called product quantization (PQ) with asymmetric querying on the FDEs [Section 3.2]. Product quantization provides significant memory savings while maintaining search quality, making the system more practical for deployment on resource-constrained hardware.

Comparative Performance Results

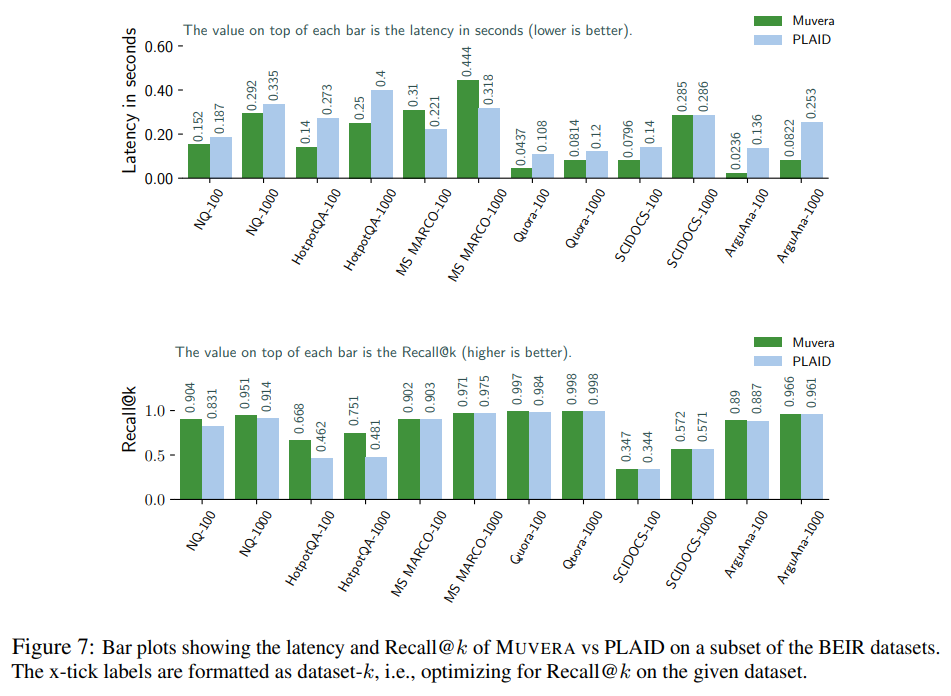
The performance comparison with PLAID, the current state-of-the-art multi-vector retrieval system, demonstrates MUVERA’s advantages across multiple metrics. We evaluated MUVERA and PLAID on the 6 datasets from the BEIR benchmark described earlier in (§3); Figure 7 shows that MUVERA achieves essentially equivalent Recall$@k$ as PLAID (within 0.4%) on MS MARCO, while obtaining up to $1.56 \times$ higher recall on other datasets [Section 3.2].


From https://arxiv.org/abs/2405.19504

We ran PLAID using the recommended settings for their system, which reproduced their recall results for MS MARCO [Section 3.2]. This careful reproduction ensures that the comparison is fair and reflects the true capabilities of both systems when properly configured.

Compared with PLAID, on average over all 6 datasets and $k \in {100, 1000}$, MUVERA achieves 10% higher Recall$@k$ (up to 56% higher), and 90% lower latency (up to $5.7 \times$ lower) [Section 3.2]. These results demonstrate that MUVERA provides both better effectiveness and better efficiency compared to existing approaches.

The consistency of MUVERA’s performance across different datasets is particularly noteworthy. Importantly, MUVERA has consistently high recall and low latency across all of the datasets that we measure, and our method does not require costly parameter tuning to achieve this [Section 3.2]. This robustness is crucial for practical deployment, where manual tuning for each dataset would be impractical.

All of our results use the same 10240-dimensional FDEs that are compressed using PQ with $PQ-256-8$; the only tuning in our system was to pick the first query beam-width over the $k$ that we rerank to match the recall obtained by PLAID [Section 3.2]. The minimal tuning required makes MUVERA much easier to deploy and maintain than competing approaches.

Memory and Compression Analysis

The practical deployment of MUVERA benefits significantly from vector compression techniques. We refer to product quantization with $C$ centers per group of $G$ dimensions as $PQ-C-G$. For example, $PQ-256-8$, which we find to provide the best tradeoff between quality and compression in our experiments, compresses every consecutive set of 8 dimensions to one of 256 centers [Section 3.2].

Thus PQ-256-8 provides $32 \times$compression over storing each dimension using a single float, since each block of 8 floats is represented by a single byte [Section 3.2]. This compression ratio dramatically reduces memory requirements while maintaining search quality, making the system practical for large-scale deployment.


From https://arxiv.org/abs/2405.19504

The compression analysis shows that product quantization not only reduces memory usage but can actually improve search performance. Using PQ-256-8 not only reduces the space usage of the FDEs by $32 \times$, but also improves the QPS at the same query beamwidth by up to $20 \times$, while incurring a minimal loss in end-to-end recall [Section 3.2]. The performance improvement comes from better cache utilization and reduced memory bandwidth requirements.

Our method has a relatively small dependence on the dataset size, which is consistent with prior studies on graph-based ANNS data structures, since the number of distance comparisons made during beam search grows roughly logarithmically with increasing dataset size [Section 3.2]. This scalability property is crucial for handling large document collections efficiently.

Practical Optimizations and Implementation Details

Ball Carving for Query Optimization

MUVERA incorporates several practical optimizations that improve real-world performance beyond the basic FDE approach. The ball carving technique addresses the computational cost of the final re-ranking step by reducing the number of query embeddings that need to be processed.

Specifically, to improve rescoring latency, we reduce the number of query embeddings by a pre-clustering stage. Specifically, we group the queries $Q$ into clusters $C_1, \ldots, C_k$, set $c_i = \sum_{q \in C_i} q$ and $Q_C = {c_1, \ldots, c_k}$ [Section C.3]. This clustering approach replaces multiple similar query embeddings with their sum, reducing computational cost while preserving semantic content.

Then, after retrieving a set of candidate documents with the FDEs, instead of rescoring via $\text{CHAMFER}(Q, P)$ for each candidate $P$, we rescore via $\text{CHAMFER}(Q_C, P)$, which runs in time $O(|Q_C| \cdot |P|)$, offering speed-ups when the number of clusters is small [Section C.3]. The time complexity reduction is proportional to the reduction in the number of query clusters.

The ball carving process uses an adaptive approach rather than fixing the number of clusters in advance. Instead of fixing $k$, we perform a greedy ball-carving procedure to allow $k$ to adapt to $Q$. Specifically, given a threshold $\tau$, we select an arbitrary point $q \in Q$, cluster it with all other points $q’ \in Q$ with $\langle q, q’ \rangle \geq \tau$, remove the clustered points, and repeat until all points are clustered [Section C.3].

The experimental analysis shows that ball carving provides significant performance improvements with minimal quality loss. Notice that for both $k = 100$ and $k = 1000$, the Recall curves flatten dramatically after a threshold of $\tau = 0.6$, and for all datasets they are essentially flat after $\tau \geq 0.7$ [Section C.3]. This indicates that aggressive clustering can be used without sacrificing retrieval quality.

For sequential re-ranking, ball carving at a $\tau = 0.7$ threshold provides a $25\%$ QPS improvement, and when re-ranking is being done in parallel (over all cores simultaneously) it yields a $20\%$ QPS improvement [Section C.3]. These performance gains demonstrate the practical value of the optimization across different computational scenarios.

Product Quantization Implementation

The product quantization implementation in MUVERA uses established techniques adapted for the specific requirements of FDE compression. We implemented our product quantizers using a simple “textbook” $k$-means based quantizer [Section C.4]. The choice of $k$-means clustering provides a good balance between compression quality and implementation simplicity.

We train the quantizer by: (1) taking for each group of dimensions the coordinates of a sample of at most 100,000 vectors from the dataset, and (2) running $k$-means on this sample using $k = C = 256$ centers until convergence [Section C.4]. The training process learns appropriate cluster centers for each dimension group, optimizing the compression for the specific data distribution.

Given a vector $x \in \mathbb{R}^d$, we can split $x$ into $d / G$ blocks of coordinates $x_{(1)}, \ldots, x_{(d / G)} \in \mathbb{R}^G$ each of size $G$. The block $x_{(i)}$ can be compressed by representing $x_{(i)}$ by the index of the centroid from the $i$-th group that is nearest to $x_{(i)}$ [Section C.4]. This block-wise compression allows fine-grained adaptation to different regions of the vector space.

Since there are 256 centroids per group, each block $x_{(i)}$ can then be represented by a single byte [Section C.4]. The single-byte representation provides exactly $32 \times$ compression when applied to groups of 8 float values, achieving the compression ratios reported in the experimental results.

The experimental evaluation of different PQ configurations reveals important insights about the compression-quality trade-off. We find that $PQ-256-8$ is consistently the best performing PQ codec across all of the datasets that we tested [Section C.4]. This configuration provides the best balance between compression ratio and approximation quality across diverse datasets.

Not using PQ at all results in significantly worse results (worse by at least $5 \times$ compared to using PQ) at the same beam width for the beam; however, the recall loss due to using $PQ-256-8$ is minimal, and usually only a fraction of a percent [Section C.4]. The performance improvement from compression comes from better memory utilization, while the minimal quality loss demonstrates the effectiveness of the quantization approach.

Conclusion

MUVERA represents a significant advance in multi-vector information retrieval by successfully bridging the gap between the high effectiveness of multi-vector models and the computational efficiency of single-vector systems. In this paper, we presented MUVERA: a principled and practical MV retrieval algorithm which reduces MV similarity to SV similarity by constructing Fixed Dimensional Encoding (FDEs) of a MV representation [Section 4].

The theoretical contributions provide the first rigorous guarantees for multi-vector retrieval approximation. We prove that FDE dot products give high-quality approximations to Chamfer similarity [Section 4]. These theoretical guarantees establish MUVERA as more than just an empirical improvement, providing mathematical foundations for understanding when and why the method works.

Experimentally, we show that FDEs are a much more effective proxy for MV similarity, since they require retrieving $2-4\times$ fewer candidates to achieve the same recall as the SV Heuristic [Section 4]. This improvement in efficiency directly translates to reduced computational costs and faster response times in practical deployment scenarios.

We complement these results with an end-to-end evaluation of MUVERA, showing that it achieves an average of $10\%$ improved recall with $90\%$ lower latency compared with PLAID [Section 4]. The combination of better effectiveness and better efficiency makes MUVERA an attractive option for upgrading existing retrieval systems.

The research acknowledges both the potential benefits and limitations of the approach. While retrieval is an important component of LLMs, which themselves have broader societal impacts, these impacts are unlikely to result from our retrieval algorithm. Our contribution simply improves the efficiency of retrieval, without enabling any fundamentally new capabilities [Section 4].

The experimental evaluation reveals some limitations that warrant further investigation. While we outperformed PLAID, sometimes significantly, on 5 out of the 6 datasets we studied, we did not outperform PLAID on MS MARCO, possibly due to their system having been carefully tuned for MS MARCO given its prevalence [Section 4].

Additionally, we did not study the effect that the average number of embeddings $m_{avg}$ per document has on retrieval quality of FDEs; this is an interesting direction for future work [Section 4]. Understanding how document length affects FDE quality could lead to adaptive approaches that optimize performance for different types of content.

The success of MUVERA opens several promising avenues for future research. Given their retrieval efficiency compared to the SV heuristic, we believe that there are still significant gains to be obtained by optimizing the FDE method, and leave further exploration of this to future work [Section 4]. The current implementation represents just the first generation of FDE-based systems, with substantial room for improvement.

The theoretical analysis suggests opportunities for extending the mathematical foundations. The approximation guarantees could potentially be tightened, and the relationship between FDE parameters and approximation quality could be better understood. This deeper theoretical understanding could lead to more principled parameter selection and better performance predictions.

The practical optimizations demonstrated in MUVERA, such as product quantization and ball carving, could be further refined and adapted for specific deployment scenarios. The interaction between these optimizations and the core FDE approach deserves deeper investigation to maximize their combined effectiveness.

The success of MUVERA on information retrieval tasks suggests potential applications to other domains that involve set-to-set similarity comparisons. Computer vision, bioinformatics, and recommendation systems all involve scenarios where the FDE approach might provide similar benefits.

References

Academic Papers and Research

Technical Articles and Blogs

programming, research

This post is licensed under CC BY 4.0 by the author.